3次インターセプトポイント(3rdIP)
久しぶりに難しい話など書きましょうか(^_^;)
無線機のカタログなどで見かける言葉に「3次インターセプトポイント」というものがあります。良く聞く言葉ですが、その正体をきちんと理解している人はそう多くないでしょう。なにせ私が勤務している会社(通信機メーカ)でさえそうなのですから。受信機を設計する上で必要な知識ですが、NFと違ってアマチュア的にはあまり定性的に語られることはありません。ここではできるだけわかりやすく、できるだけ具体的計算例も交えて、3rdIPとはどんなものか説明したいと思います。
1. n次インターセプトポイント(IP)とn次混変調歪(IMD)

|
混変調の話のところで3rdIPとはどんなものか説明していますが、あらためて解説しておきます。
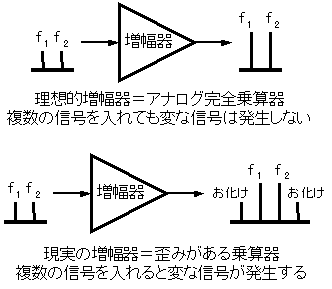
増幅器は入力された信号を増幅率倍に増幅して出力します。例えば電圧増幅率がG倍の増幅器に周波数f1[Hz]、振幅1[V]の入力を入れたとすると、出力には周波数f1[Hz]、振幅G[V]の信号が出てきます。増幅器は倍数固定のアナログ乗算器ってわけです。では入力信号が2つあった場合はどうでしょう? 片方の信号は周波数f1[Hz]、振幅A1[V]、もう片方の信号は周波数f2[Hz]、振幅A2[V」とします。アナログ乗算器なのでそれぞれの信号の振幅がG倍になるだけなので、出力には周波数f1[Hz]、振幅A1G[V]の信号と周波数f2[Hz]、振幅A2G[V]の信号が出てきます。単純ですね。
しかし、これは理想化されたモデルの話で、現実の増幅器ではこうはいきません。世の中にある増幅器は入力と出力はほぼ比例関係にありますが完全ではありません(非直線性成分を含んでいる)。このような場合、複数の信号を入力すると入力には無い周波数に信号が出力に発生します。これを「相互変調歪」とか「混変調歪」と言います。英語ではInterModulation Distortion、略してIMDです。出てくる周波数は不規則なわけではなく、以下のような式で計算できます。
±m×f1±n×f2 ただしm,n = 0, 1, 2, 3・・・・・・・
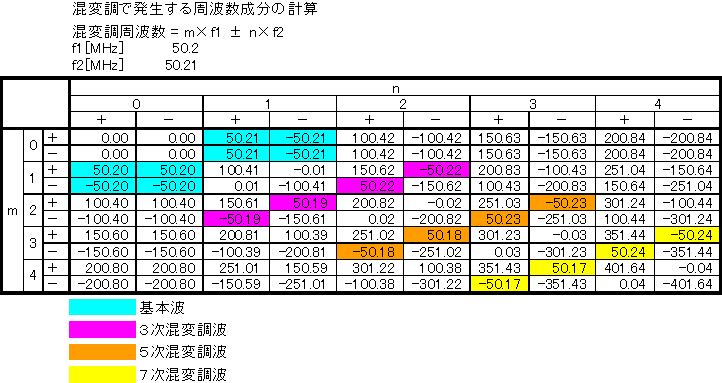
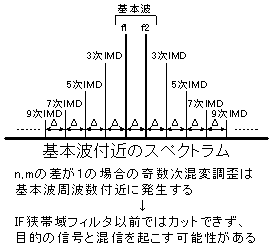
|m|+|n|(m,nの絶対値)の組み合わせで表される周波数の混変調歪を|m|+|n|次混変調歪と呼びます。例えば m = ±1 & n = ±1 を2次混変調歪、m = ±1 & n = ±2 及び m = ±2 & n = ±1 を3次混変調歪と呼びます。1次は自分自身なので除外し、2次、3次、4次・・・・と連なります。m,nは無限に続くので混変調歪は無限にあることになりますが、実際には次数が高くなると減衰するので、よほど歪んだ領域で増幅器を使わない限りは3,4次程度まで考慮すれば問題ありません。
f1=50.2MHz、f2=50.21MHzとした場合の8次混変調歪までの周波数を計算した結果を示します。一般的にRF回路にはフィルタが挿入されているので、変な周波数信号が発生してもフィルタで減衰されるのでさほど問題になりませんが、使用帯域内に発生する混変調はフィルタを通り抜けるので問題になります。見ておわかりの通り、偶数次の混変調歪は50MHzから遠い周波数に発生するためフィルタで切り落とせるのであまり問題になりませんが、n,mの差が1で3,5,7・・・・・の奇数次混変調歪は元の信号周波数付近に落ち込んできてしまい、特に3次混変調歪はレベルが大きく最も問題になります。上記計算表の例では、例えば交信相手が50.19MHzにいて、50.2MHzと50.21MHzに別の局が電波を出していた場合、その2局による3次混変調歪の周波数が50.19MHzに発生するため混信になってしまいます。このような状況は特にコンテストのようにたくさんの強い局がいっぺんに出ているときに発生しやすく、ハンディー機等の混変調に弱い無線機では3次混変調歪による「お化け」がバンド内のあちこちに聞こえます。
 |
 |
ついでのお話し。奇数次混変調歪が元の周波数近くに落ち込むので問題になると話しましたが、2次混変調歪が問題になる場合があります。それは受信機では最初のフィルタを切り替えるのにダイオードスイッチを使っている場合です。ダイオードスイッチは半導体なので電力を上げていくと飽和するレベルがあり、増幅回路のようにIPがあります。そしてフィルタ入力側では帯域を制限する物はアンテナだけで、様々な放送波(非常に強力)も含めて非常に広い周波数範囲の信号が入ってきます。そうするとそれらの間で2次混変調歪が発生し、偶然にも受信周波数に乗ってしまうことがあります。50MHzの場合では2つの周波数の差が50MHzになる関係、もしくは2つの周波数の和が50MHzになる関係の電波で2次混変調歪が発生すると妨害を受けます。ですから非線形歪を持つ回路で広帯域を扱う場合は2次混変調歪にも注意する必要があります。
2. 3次インターセプトポイント(3rdIP)の測定方法
|
n次IPの一般的な測定方法を示します。SGを2台用意し、周波数を僅かにずらしてレベルを同じにして増幅器に入れます。当然ながら増幅器の出力には同じレベルで周波数が異なる2つのキャリアが出てきますが、同時に両脇にn次混変調歪が発生します。混変調歪のレベルPn[dBm]と基本波出力のレベルPo[dBm]を測定し、以下の式で計算することにより増幅器のn次IP[dBm]を求めることができます。
Po - Pn
IPn = Po + ────
n - 1
3次混変調の場合は n = 3 なので以下のようになります。
Po -
P3
IP3 = Po + ────
2
= (3Po - P3)/2
この式から3次混変調歪のレベルを求める式に変形すると以下のようになります。
P3 = 3×Po - 2×IP3
つまり、3次混変調歪レベルは出力の3倍に比例して増加します。これは対数表記での話ですので、現実の真数の世界では3乗となります。つまり、3次混変調歪レベルは基本波出力レベルの3乗に比例して急激に増加します。例えば受信電波強度が10倍になったら、それに伴って発生する3次混変調歪は1000倍に増加します! 基本波は入力に比例して増加しますので3次混変調歪の増加ぶりが分かるでしょう。3次混変調歪を低く抑えるにはIPの高い増幅器を使用するか、基本波出力レベルPoを抑えて使うかのいずれかしかありません。もっとも、最近ではDSPを使用して歪みを打ち消して等価的にIPを高くする方式も存在しますが、回路が複雑でアマチュア的には手が届かないでしょう。1つの増幅器で複数のキャリアを増幅する携帯電話基地局のファイナル増幅器などに応用されています。

|
上記の3rdIPに関する式をグラフに表したものがよく見る図です。図にしてみると3rdIPとは基本波出力の延長線と3次混変調歪延長線の交点になります。関係する式もまとめて示しておきました。この中で出てくるOPIPやIPIPは後ほど説明します。
3. 3rdIPとP1dBの関係
3rdIP、P1dBとも最大出力(飽和出力)に関係する値で、飽和レベルが大きい増幅器ほど3rdIP、P1dBとも大きくなりますが、おおよその傾向として以下のような関係があります。
3rdIP = P1dB + 10dB
モノによって数dBのばらつきはありますが、3rdIPはP1dBの10dB上にあると考えることは「当たらずしも遠からず」で、アマチュア的には差し支えありません。P1dBまでがほぼ歪み無く増幅できる出力電力と見なしていいでしょう。ということは3rdIP=+30[dBm]の増幅器だったら出力=+20[dBm]程度までは出せると見なせるわけです。
4. IPIPとOPIP
3rdIPの説明図において、2つの直線が交わる交点はグラフのX軸(入力レベル)及びY軸(出力レベル)の両側から読むことができます。一般的に3rdIPと呼ばれている数字は出力レベル側を読んだ数字で、Outputの略をくっつけてOPIPと表したりします。一方、入力側を呼んだ数字はInputの略をくっつけてIPIPと表したりします。OPIPとIPIPは同じものを違った切り口で見ているだけですが、実は深い意味を持っていたりもしますので説明しておきます。
OPIPは出力側の数字なので「ここまで出力が出せる」というような、言ってみれば送信側の物の見方です。送信電力が決まればそれに見合ったOPIPの増幅器を選んで歪まないようにします。一方のIPIPは入力側の数字なので「ここまで入れても歪まない」というような、言ってみれば受信側の物の見方です。受信レベルが分かっている場合には(プロの世界では無線通信を行う場合は回線設計を行うのであらかじめ受信レベルがどのくらいか分かっている)そのレベルを入れても飽和しないようなIPIP仕様値とします。
以上のように送信系と受信系では3rdIPと言ってもOPIPとIPIPを使い分けないと問題が発生します。一般的に増幅器の3rdIPはOPIPで表されるため受信系では要注意です。
ちなみにグラフを見て分かるとおり、OPIPとIPIPの間には次の関係があります。単純ですね。
IPIP[dBm] = OPIP[dBm] - Gain[dB]
式は簡単ですが、設計上ではちょっとだけ注意点があります。普通、増幅器の利得の仕様は最低値が記載されていますし、自分で設計する場合も最低何dBと仕様を決めますが、IPの観点から言うと利得が仕様より高いってことは計算値よりIPIPが低下することを意味します。NFやレベルの点から言えば利得が高いことは問題ないのですがIPが低下してしまうため、最終的にはNFに影響がないような場所にアッテネータを入れて利得調整が必要になります。普通、データシートでは利得上限仕様値なんて書いてありませんから、こればかりは組み立ててみなくてはわかりません。
もひとつオマケ。データシートに記載された増幅器等の3rdIPは「仕様値」ではなく「ティピカル値」の場合があるので要注意。仕様値=最悪値なので、現物は絶対に記載値以上の3rdIPがありますが、ティピカル値の場合は標準的にはこの程度ですというイメージで性能を保証するものではありません。できればそのようなデバイスは避けた方がいいですが、どうしても使わざるを得ないことも多く、実験を行って実力を見て、ある程度のマージンを確保して使用します。
5. 直列回路の合成3rdIP(IPIP)
いくつかの増幅器が直列接続されたときの合成3rdIPの計算方法を知っていますか? 増幅器直列接続時の合成雑音指数の計算方法は教科書にも載っていますが、なぜか3rdIPについては載っていません。いや、それどころか学校の通信の授業では雑音指数は出てきても3rdIPや飽和レベルの話は全く出てこなかったような・・・。仕事の関係で電子回路の参考書類も色々と見ていますが、どれにも書いてありません。理由は全く不明。雑音指数の場合と同様に、システム設計上必要な知識のはずなんですが・・・・。受信系では3rdIPは雑音指数と並んで重要な性能の一つで、いくつもの回路を組み合わせて受信系を組み上げるのが普通ですから、カスケード接続時の3rdIPの計算は必需品のはず。なぜ知られていないのか不思議でなりません。
ちなみに海外のマイクロ波部品カタログには豆知識のページがあり、3rdIPについて詳しく書いてあるものがあり、そこで得た知識が私のベースになっています。そのカタログとはWJ(ワトキンス・ジョンソン)のものでした。ただし、そこでも直列回路の合成3rdIPについては書かれていませんでした。私がその計算方法を目にした唯一の資料は、アメリカの会社が設計を担当した、あるマイクロ波通信システムのシステム設計資料だけでした。この資料は通信(特に受信)システムのシステム設計資料としては大変優秀で、それこそ教科書以上のことを教えてくれるものでした。もう20年近く昔の資料ですが、システム設計とは言うなれば「システム仕様を決めるための設計」なのでデバイスが進歩して性能が上がろうとも設計の考え方は不変で、今の設計なら昔より性能が上がるでしょうけどシステム設計方法は変わりません。
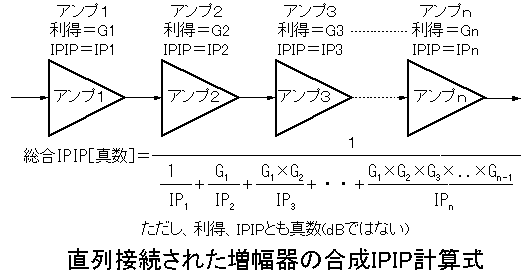
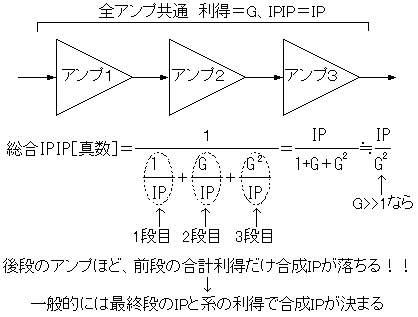
さて本題に戻りましょう。直列回路の合成IPIPは各増幅器の利得とIPIPで決まり、以下の式で計算できます。ただし、この式の利得、IPIPの値は対数表示[dB]ではなく真数表示とします。つまりIPIPの単位としては[W](もしくは[mW])、利得(無単位)は*dBではなく*倍とします。
1
総合IPIP[真数]=──────────────────────────
1 G1 G1×G2
G1×G2×G3×..×Gn-1
──+──+────+・・+──────────
IP1 IP2
IP3
IPn
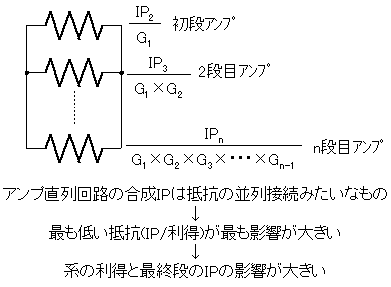
どこかで見たことがある形式の分数ですね〜。そう、抵抗を並列接続したときの合成抵抗計算式とほぼ同じです。この計算式の特徴は、合成抵抗は最も低い抵抗よりも必ず低くなることと、各抵抗の中で飛び抜けて抵抗値が低いものがあったとすると、合成抵抗はほぼその抵抗と同じになることです。これは逆数の和の逆数なので当然ですね。逆数の和の計算では値が小さなものほど逆数にしたとき大きな値になるので、他の逆数を無視できます。その逆数を取るのですから元の値と似たり寄ったりになります。もちろん、同じ値の抵抗が並列接続された場合は平等に効果を発揮し、2並列なら1/2、5並列なら1/3になります。
|
|
|
しかし、合成IPIPでは抵抗の並列接続と決定的に異なる点があります。それは、後段の増幅器ほど前段増幅器の利得の合計分だけIPIPが低下したのと同等になることです。この意味は同じ性能の増幅器を直列したときの計算結果を考えればすぐに理解できます。3つの増幅器を直列接続した場合は抵抗の3並列接続に相当しますが、抵抗のように元の抵抗値の1/3にはなりません。式の分母を見てみると、2段目の増幅器に該当する項は1段目の増幅器の利得分大きくなり、3段目ともなると1,2段目の増幅器の合計利得だけ大きくなってしまい、利得が20dBとかのように1より充分大きな値だった場合は、1,2段の項は相対的に小さすぎて3段目の項だけで結果が決まってしまいます。最終結果は1,2段目の合計利得の2乗に比例して小さくなります。つまり、劇的に3rdIPが低下します。まあ、これはよく考えてみれば当たり前の話で、出力飽和電力は1個の増幅器の時と変わりがないのに利得は3倍(正確には元の3乗)に増加したのですから、飽和してしまう入力レベルは1/3になるのです。こうなると先述した式のように3次混変調歪が増加します。受信系でも帯域内にある雑音と受信信号の合計がそれなりの電力になる場所では、増幅器を直列接続するときには後段ほど高いIPの増幅器を使わないといけません。
上記の式を用いればどれくらいの入力があった場合にどれくらいの混変調歪が発生するのか、簡単に言えば受信機の混変調に対する強さが事前に計算できます。そのためには各増幅回路の利得とIPIP(OPIPでもいい)をしっかりと把握するのが大切です。
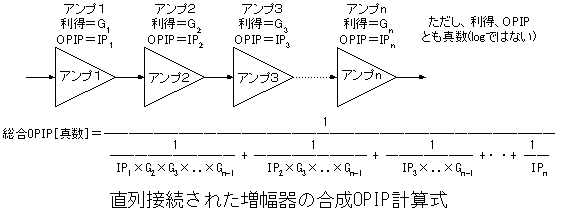
ついでに、今まではIPIPでの話ですが、この計算はOPIPにも当てはまります。ただ、OPIPは送信系の考え方なので、式もちょっと変わります。でも、計算してみれば分かりますが両者は等価です。
1
総合OPIP[真数]=─────────────────────────────────────
1 1
1 1
────────── + ───────── + ─────── +・・+ ──
IP1×G2×G3×..×Gn-1
IP2×G3×..×Gn-1 IP3×..×Gn-1
IPn
|
|
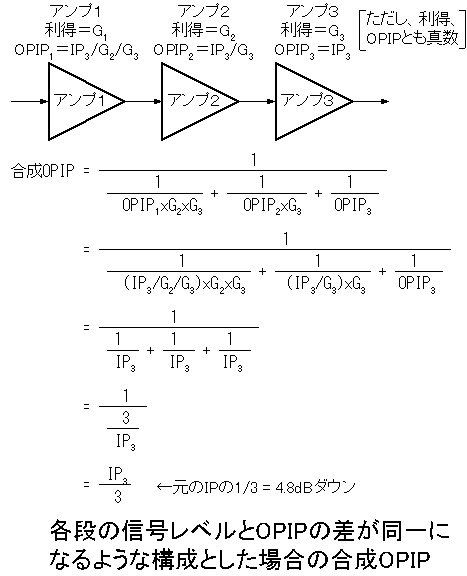
出力換算なので、ファイナル増幅器のOPIPは直接効いてきます。前段部分はそれより後段の増幅器による利得だけOPIPが上がったように見えます。通常、アマチュア無線での送信系では送信電波は1波だけなので、よほど歪みが多い飽和領域付近で使わない限りは3次混変調歪が問題になることはなく、設計では各段で飽和しないようにレベル配分に気を付ければいいだけですが、携帯電話基地局のようにいくつものキャリアを同時に増幅するとなると話が変わります。今はCDMAが広まってきましたが、第2世代以前の携帯電話はFDMAで等周波数間隔で通話チャネルが並んでおり、隣接するチャネル間での3次混変調歪は隣接チャネルと同じ周波数となって混信してしまうのです。そのため、基地局増幅器は非常に厳しい直線性が要求されます。単純に飽和レベルに気を付けて各段の増幅器を設計し、どの増幅器も最大出力時に同じバックオフ(飽和レベルから何dB下で動かすか)で動作させるとした場合、合計OPIPはファイナル増幅器のOPIPより低下します。もし2段なら-3dB、4段なら-6dBダウンです。これは実際に計算式をやってみれば分かります(図を参照)。厳密な結果が求められる場合は、送信側でも合成IPを計算すべきです。単純にファイナルだけで考えてしまうと予想以上の3次混変調歪が発生する可能性があります。
6. 直列回路における3rdIPとNFの関係
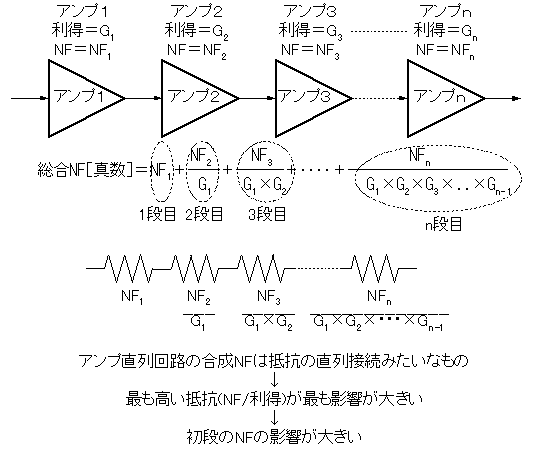
先述のように、直列回路の3rdIPは、後段増幅器のIPが前段増幅器の利得分だけ低下したのと等価なことが分かりました。ではNFはどうでしょうか? 直列回路のNFは以下の式で求められます。
NF2
NF3 NFn
総合NF[真数] = NF1 + ── + ─── +
・・・・ + ──────────
G1 G1×G2 G1×G2×G3×..×Gn-1
|
3rdIPの時は逆数の和の逆数でしたが、NFではシンプルな式で表現されます。各項が各増幅器が総合NFに与える影響で、後段の増幅器ほど前段増幅器の利得分だけNFが小さくなるので、初段増幅器の利得が高いほど後段の影響が無くなります。つまり、NFにとっては初段利得は大きいほど良いわけです。衛星通信のような回線C/Nがギリギリで通信を行う場合のプリアンプ利得は60dB(電力利得が100万倍!)くらいが普通で、後段のNFの影響は100万分の1に低減されるのでほぼ無視でき、初段のNFが全体のNFになります。
しかし、3rdIPにとっては話が逆になります。初段の利得が60dBの場合、後段の3rdIPは60dB低下するのと同じなので、初段のIPと比較して非常に低い値となり、初段のIPとは無関係に後段側のIPで全体のIPが決まってしまいます。
つまり、感度を良くするには初段の利得を上げるのが有利ですが、そうすると3rdIPが低下して混変調に弱くなることを意味します。つまり、感度と混変調特性は「あちらを立てればこちらが立たず」の相反する関係にあり、両立させることは簡単ではないのです。両者を高いレベルでバランスさせるのがシステム設計者の腕に見せ所とも言えます。もちろん、コストとの兼ね合いがありますので、何でもできるわけではありませんが。
このように系の利得が上がるとその分だけ3rdIPが低下するので、安易にプリアンプを追加するのは賢明とは言えません。もし利得=20dBのプリアンプならIPは20dB低下し、同じ受信レベルの信号を受けたときに発生する3次混変調歪は3×20dB=60dB上昇します(現実にはAGCが働いて受信機利得が低下するのでそこまでは出ないはずだけど)。周囲の電波環境が良くて混変調を生じる強力な電波が無い場合はプリアンプは有効ですが、都市部でたくさんの局が出ている場所でプリアンプを使うと3次混変調歪によるお化けやガサガサした音が聞こえる可能性の方が高そうです。
DE JS1MLQ